March 22nd, 2023 by Karen Grace-Martin
If you have a categorical predictor variable that you plan to use in a regression analysis in SPSS, there are a couple ways to do it.
You can use the SPSS Regression procedure. Or you can use SPSS General Linear Model–>Univariate, which I discuss here. If you use Syntax, it’s the UNIANOVA command.
The big question in SPSS GLM is what goes where. As I’ve detailed in another post, any continuous independent variable goes into covariates. And don’t use random factors at all unless you really know what you’re doing.
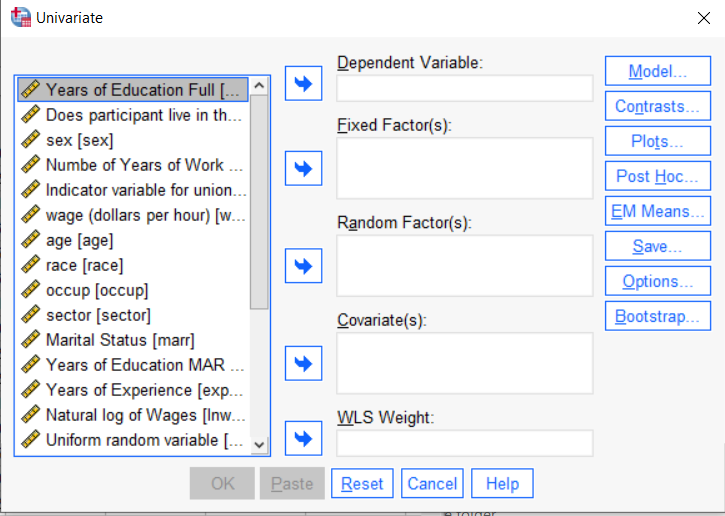
So the question is what to do with your categorical variables. You have two choices, and each has advantages and disadvantages.
The easiest is to put categorical variables in Fixed Factors. SPSS GLM will dummy code those variables for you, which is quite convenient if your categorical variable has more than two categories.
However, there are some defaults you need to be aware of that may or may not make this a good choice.
The dummy coding reference group default
SPSS GLM always makes the reference group the one that comes last alphabetically.
So if the values you input are strings, it will be the one that comes last. If those values are numbers, it will be the highest one.
Not all procedures in SPSS use this default so double check the default if you’re using something else. Some procedures in SPSS let you change the default, but GLM doesn’t.
In some studies it really doesn’t matter which is the reference group.
But in others, interpreting regression coefficients will be a whole lot easier if you choose a group that makes a good comparison such as a control group or the most common group in the data.
If you want that to be the reference group in SPSS GLM, make it come last alphabetically. I’ve been known to do things like change my data so that the control group becomes something like ZControl. (But create a new variable–never overwrite original data).
It really can get confusing, though, if the variable was already dummy coded–if it already had values of 0 and 1. Because 1 comes last alphabetically, SPSS GLM will make that group the reference group and internally code it as 0.
This can really lead to confusion when interpreting coefficients. It’s not impossible if you’re paying attention, but you do have to pay attention. It’s generally better to recode the variable so that you don’t confuse yourself. And while you may believe you’re up for overcoming the confusion, why make things harder on yourself or with any other colleague you’re sharing results with?
Interactions among fixed factors default
There is another key default to keep in mind. GLM will automatically create interactions between any and all variables you specify as Fixed Factors.
If you put 5 variables in Fixed Factors, you’ll get a lot of interactions. SPSS will automatically create all 2-way, 3-way, 4-way, and even a 5-way interaction among those 5 variables.
That’s a lot of interactions.
In contrast, GLM doesn’t create by default any interactions between Covariates or between Covariates and Fixed Factors.
So you may find you have more interactions than you wanted among your categorical predictors. And fewer interactions than you wanted among numerical predictors.
There is no reason to use the default. You can override it quite easily.
Just click on the Model button. Then choose “Custom Model.” You can then choose which interactions you do, or don’t, want in the model.
If you’re using SPSS syntax, simply add the interactions you want to the /Design subcommand.
So think about which interactions you want in the model. And take a look at whether your variables are already dummy coded.
February 21st, 2023 by Karen Grace-Martin
Interpreting the Intercept in a regression model isn’t always as straightforward as it looks.
Here’s the definition: the intercept (often labeled the constant) is the expected value of Y when all X=0. But that definition isn’t always helpful. So what does it really mean?
Regression with One Predictor X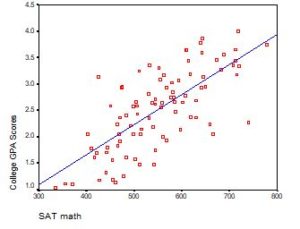
Start with a very simple regression equation, with one predictor, X.
If X sometimes equals 0, the intercept is simply the expected value of Y at that value. In other words, it’s the mean of Y at one value of X. That’s meaningful.
If X never equals 0, then the intercept has no intrinsic meaning. You literally can’t interpret it. That’s actually fine, though. You still need that intercept to give you unbiased estimates of the slope and to calculate accurate predicted values. So while the intercept has a purpose, it’s not meaningful.
Both these scenarios are common in real data. (more…)
December 8th, 2022 by Karen Grace-Martin
Have you ever had this happen? You run a regression model. It can be any kind—linear, logistic, multilevel, etc. In the ANOVA table, the effect of interest has a very low p-value. In the regression table, it doesn’t. Or vice-versa.
How can the same effect have two different p-values? In this article, let’s explore when this happens and what it means.
What the statistics in each table measures
The ANOVA table is a table of F tests. It may not be called the ANOVA table on your output, but it always includes a set of F tests. Some software procedures only give one F test for the model as a whole, but most will break it down into a series of F tests, one for each predictor variable or term in your model.
The regression coefficients table is a table of t tests. It includes each regression coefficient, along with its standard error, and usually a t test (some generalized linear models will have Wald or z tests instead, but they have the same role here).
Both tables often list out each predictor variable, along with a p-value for that variable’s conditional effect on Y.
There are two situations in which the p-values will match. Both must be true.
- The F test has one df. This happens in two situations. Either the predictor, X, is numerical or it’s categorical and binary (only two groups).
- The predictor is not involved with any interactions with a variable that is not centered at is mean.
If both of those are true, not only will the p-value match, but the t-statistic in the regression coefficients table will be the positive or negative square root of the F statistic.
An Example ANOVA Table with Matching and Unmatching Regression Coefficients
Here’s an example of an ANOVA table from a linear regression. In this example, there are four treatment groups, two genders, and age in years (measured continuously and centered at its mean). The response variable, Y, is a satisfaction score with a training. The four groups represented four learning strategies the adult learners were trained to use.
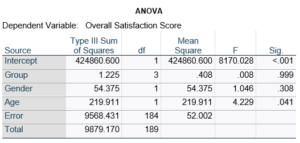
Let’s compare this to the regression coefficients table.
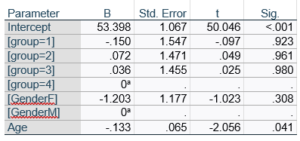
If you compare p-values across the two tables, you can see that Gender and Age have the same p-values, but Group doesn’t.
Gender and Age meet both conditions. Both have 1 df in the F table. Gender because it’s binary (two categories) and Age because it’s numerical). There are no interactions.
Group doesn’t match because it has 3 df in the F test. The F test is testing the null hypothesis that there is no difference among the four means. The t-tests in the regression coefficients table are testing three specific contrasts. Each one compares one group mean to the group 4 mean. For example, the group=1 coefficient tests whether the difference between the mean group 1 satisfaction score differs only from the group 4 score. It’s a different null hypothesis than the F test.
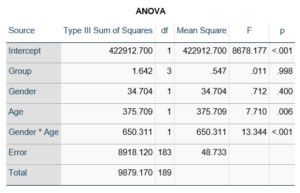
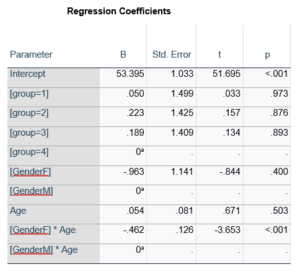
This would be the case whether or not there were interactions in the model that contain Group. Any time you have more that one df in the F test (you can see group has 3), you’ll get as many p-values in the regression coefficients as you have df in the F table. The p-values can’t match because there are more of them in the regression coefficients table.
Gender, which is also categorical, does have the same p-value in both tables. It has 1 df in the F test, which tests the null hypothesis that the two gender means have no variance (they’re the same). Gender is involved in an interaction, so the only reason the hypothesis test, and therefore the p-value, is the same is because the variable it interacts with, Age, is centered.
In conclusion, most of the time, it’s fine if the results don’t match. It’s because the two tables are reporting results of different hypothesis tests, based on what’s in your model.
December 20th, 2021 by Karen Grace-Martin
Updated 12/20/2021
Despite its popularity, interpreting regression coefficients of any but the simplest models is sometimes, well….difficult.
So let’s interpret the coefficients in a model with two predictors: a continuous and a categorical variable. The example here is a linear regression model. But this works the same way for interpreting coefficients from any regression model without interactions.
A linear regression model with two predictor variables results in the following equation:
Yi = B0 + B1*X1i + B2*X2i + ei.
The variables in the model are:
- Y, the response variable;
- X1, the first predictor variable;
- X2, the second predictor variable; and
- e, the residual error, which is an unmeasured variable.
The parameters in the model are:
- B0, the Y-intercept;
- B1, the first regression coefficient; and
- B2, the second regression coefficient.
One example would be a model of the height of a shrub (Y) based on the amount of bacteria in the soil (X1) and whether the plant is located in partial or full sun (X2).
Height is measured in cm. Bacteria is measured in thousand per ml of soil. And type of sun = 0 if the plant is in partial sun and type of sun = 1 if the plant is in full sun.
Let’s say it turned out that the regression equation was estimated as follows:
Y = 42 + 2.3*X1 + 11*X2
Interpreting the Intercept
B0, the Y-intercept, can be interpreted as the value you would predict for Y if both X1 = 0 and X2 = 0.
We would expect an average height of 42 cm for shrubs in partial sun with no bacteria in the soil. However, this is only a meaningful interpretation if it is reasonable that both X1 and X2 can be 0, and if the data set actually included values for X1 and X2 that were near 0.
If neither of these conditions are true, then B0 really has no meaningful interpretation. It just anchors the regression line in the right place. In our case, it is easy to see that X2 sometimes is 0, but if X1, our bacteria level, never comes close to 0, then our intercept has no real interpretation.
Interpreting Coefficients of Continuous Predictor Variables
Since X1 is a continuous variable, B1 represents the difference in the predicted value of Y for each one-unit difference in X1, if X2 remains constant.
This means that if X1 differed by one unit (and X2 did not differ) Y will differ by B1 units, on average.
In our example, shrubs with a 5000/ml bacteria count would, on average, be 2.3 cm taller than those with a 4000/ml bacteria count. They likewise would be about 2.3 cm taller than those with 3000/ml bacteria, as long as they were in the same type of sun.
(Don’t forget that since the measurement unit for bacteria count is 1000 per ml of soil, 1000 bacteria represent one unit of X1).
Interpreting Coefficients of Categorical Predictor Variables
Similarly, B2 is interpreted as the difference in the predicted value in Y for each one-unit difference in X2 if X1 remains constant. However, since X2 is a categorical variable coded as 0 or 1, a one unit difference represents switching from one category to the other.
B2 is then the average difference in Y between the category for which X2 = 0 (the reference group) and the category for which X2 = 1 (the comparison group).
So compared to shrubs that were in partial sun, we would expect shrubs in full sun to be 11 cm taller, on average, at the same level of soil bacteria.
Interpreting Coefficients when Predictor Variables are Correlated
Don’t forget that each coefficient is influenced by the other variables in a regression model. Because predictor variables are nearly always associated, two or more variables may explain some of the same variation in Y.
Therefore, each coefficient does not measure the total effect on Y of its corresponding variable. It would if it were the only predictor variable in the model. Or if the predictors were independent of each other.
Rather, each coefficient represents the additional effect of adding that variable to the model, if the effects of all other variables in the model are already accounted for.
This means that adding or removing variables from the model will change the coefficients. This is not a problem, as long as you understand why and interpret accordingly.
Interpreting Other Specific Coefficients
I’ve given you the basics here. But interpretation gets a bit trickier for more complicated models, for example, when the model contains quadratic or interaction terms. There are also ways to rescale predictor variables to make interpretation easier.
So here is some more reading about interpreting specific types of coefficients for different types of models:
October 11th, 2021 by Karen Grace-Martin
One issue that affects how to interpret regression coefficients is the scale of the variables. In linear regression, the scaling of both the response variable Y, and the relevant predictor X, are both important.
In regression models like logistic regression, where the response variable is categorical, and therefore doesn’t have a numerical scale, this only applies to predictor variables, X.
This can be an issue of measurement units–miles vs. kilometers. Or it can be an issue of simply how big “one unit” is. For example, whether one unit of annual income is measured in dollars, thousands of dollars, or millions of dollars.
The good news is you can easily change the scale of variables to make it easier to interpret their regression coefficients. This works as well for functions of regression coefficients, like odds ratios and rate ratios.
All you have to do is create a new variable in your data set (don’t overwrite the individual one in case you make a mistake). This new variable is simply the old one multiplied or divided by some constant. The constant is often a factor of 10, but it doesn’t have to be. Then use the new variable in your model instead of the original one.
Since regression coefficients and odds ratios tell you the effect of a one unit change in the predictor, you should multiply them so that a one unit change in the predictor makes sense.
An Example of Rescaling Predictors
Here is a really simple example that I use in one of my workshops.
Y= first semester college GPA
X1= high school GPA
X2=SAT score
High School and first semester College GPA are both measured on a scale from 0 to 4. If you’re not familiar with this scaling, a 0 means you failed a class. An A (usually the top possible score) is a 4, a B is a 3, a C is a 2, and a D is a 1. So for a grade point average, a one point difference is very big.
If you’re an admissions counselor looking at high school transcripts, there is a big difference between a 3.7 GPA and a 2.7 GPA.
SAT score is on an entirely different scale. It’s a normed scale, so that the minimum is 200, the maximum is 800, and the mean is 500. Scores are in units of 10. You literally cannot receive a score of 622. You can get only 620 or 630.
So a one-point difference is not only tiny, it’s meaningless. Even a 10 point difference in SAT scores is pretty small. But 50 points is meaningful, and 100 points is large.
If you leave both predictors on the original scale in a regression that predicts first semester GPA, you get the following results:
Let’s interpret those coefficients.
The coefficient for high school GPA here is .20. This says that for each one-unit difference in GPA, we expect, on average, a .2 higher first semester GPA. While a one-unit change in GPA is huge, that’s reasonably meaningful.
The coefficient for SAT math scores is .002. That looks tiny. It says that for each one-unit difference in SAT math score, we expect, on average, a .002 higher first semester GPA. But a one-unit difference in SAT score is too small to interpret. It’s too small to be meaningful.
So we can change the scaling of our SAT score predictor to be in 10-point differences. Or in 100 point differences. Chose the scale for which one unit is meaningful.
Changing the scale by mulitplying the coefficient
In a linear model, you can simply multiply the coefficient by 10 to reflect a 10-point difference. That’s a coefficient of .02. So for each 10 point difference in math SAT score we expect, on average, a .02 higher first semester GPA.
Or we could multiply the coefficient by 50 to reflect a 50-point difference. That’s a coefficient of .10. So for each 50 point difference in math SAT score we expect, on average, a .1 higher first semester GPA.
When it’s easier to just change the variables
Multiplying the coefficient is easier than rescaling the original variable if you only have one or two of these and you’re using linear regression.
It doesn’t work once you’ve done any sort of back-transformation in generalized linear models. So you can’t just multiply the odds ratio or the incidence rate ratio by 10 or 50. Both of these are created by exponentiating the regression coefficient. Because of the order of operations in algebra, You have to first multiply the coefficient by the constant, and then re-expontiate.
Likewise, if you are using this predictor in more than one linear regression model, it’s much simpler to rescale the variable in the first place. Simply divide that SAT score by 10 or 50 and the coefficient will .02 or .10, respectively.
Updated 12/2/2021
April 9th, 2021 by Karen Grace-Martin
Centering a covariate –a continuous predictor variable–can make regression coefficients much more interpretable. That’s a big advantage, particularly when you have many coefficients to interpret. Or when you’ve included terms that are tricky to interpret, like interactions or quadratic terms.
For example, say you had one categorical predictor with 4 categories and one continuous covariate, plus an interaction between them.
First, you’ll notice that if you center your covariate at the mean, there is (more…)
