A well-fitting regression model results in predicted values close to the observed data values. The mean model, which uses the mean for every predicted value, generally would be used if there were no useful predictor variables. The fit of a proposed regression model should therefore be better than the fit of the mean model. But how do you measure that model fit?
Measures of Model Fit
Three statistics are used in Ordinary Least Squares (OLS) regression to evaluate model fit: R-squared, the overall F-test, and the Root Mean Square Error (RMSE).
All three are based on two sums of squares: Sum of Squares Total (SST) and Sum of Squares Error (SSE).
SST measures how far the data are from the mean, and SSE measures how far the data are from the model’s predicted values. Different combinations of these two values provide different information about how the regression model compares to the mean model.
R-squared
The difference between SST and SSE is the improvement in prediction from the regression model, compared to the mean model. Dividing that difference by SST gives R-squared. It is the proportional improvement in prediction from the regression model, compared to the mean model. It indicates the goodness of fit of the model.
R-squared has the useful property that its scale is intuitive. It ranges from zero to one.
Zero indicates that the proposed model does not improve prediction over the mean model. One indicates perfect prediction. Improvement in the regression model results in proportional increases in R-squared.
One pitfall of R-squared is that it can only increase as predictors are added to the regression model. This increase is artificial when predictors are not actually improving the model’s fit. To remedy this, a related statistic, Adjusted R-squared, incorporates the model’s degrees of freedom.
Adjusted R-squared
Adjusted R-squared will decrease as predictors are added if the increase in model fit does not make up for the loss of degrees of freedom. Likewise, it will increase as predictors are added if the increase in model fit is worthwhile.
Adjusted R-squared should always be used with models with more than one predictor variable. It is interpreted as the proportion of total variance that is explained by the model.
There are situations in which a high R-squared is not necessary or relevant. When the interest is in the relationship between variables, not in prediction, the R-squared is less important.
An example is a study on how religiosity affects health outcomes. A good result is a reliable relationship between religiosity and health. No one would expect that religion explains a high percentage of the variation in health, as health is affected by many other factors. Even if the model accounts for other variables known to affect health, such as income and age, an R-squared in the range of 0.10 to 0.15 is reasonable.
The F-test
The F-test evaluates the null hypothesis that all regression coefficients are equal to zero versus the alternative that at least one is not. An equivalent null hypothesis is that R-squared equals zero.
A significant F-test indicates that the observed R-squared is reliable and is not a spurious result of oddities in the data set. Thus the F-test determines whether the proposed relationship between the response variable and the set of predictors is statistically reliable. It can be useful when the research objective is either prediction or explanation.
RMSE
The RMSE is the square root of the variance of the residuals. It indicates the absolute fit of the model to the data–how close the observed data points are to the model’s predicted values. Whereas R-squared is a relative measure of fit, RMSE is an absolute measure of fit. As the square root of a variance, RMSE can be interpreted as the standard deviation of the unexplained variance. It has the useful property of being in the same units as the response variable.
Lower values of RMSE indicate better fit. RMSE is a good measure of how accurately the model predicts the response. It’s the most important criterion for fit if the main purpose of the model is prediction.
Which Model Fit Statistic?
The best measure of model fit depends on the researcher’s objectives, and more than one are often useful. The statistics discussed above are applicable to regression models that use OLS estimation.
Many types of regression models, however, such as mixed models, generalized linear models, and event history models, use maximum likelihood estimation. These statistics are not available for such models.
Hi,
How would one compare the fit of a model with Ln(y) as the dependent variable to the fit of a model with just y as the dependent variable?
Thanks,
Scarlett
Rohan raised a very good point. RMSE by itself does not tell whether your estimations are good! Suppose you are estimating the minimum temperature of a place where its variation is 0-5 C. Then if your RMSE is around 1, your estimations are good. But if you are estimating the mean sea level pressure of the same region expecting to get the RMSE of 1 is something like a kid asking for the moon. In this case, an RMSE of a few hundred is good enough. Now, to judge whether your SMSE of a few hundred is good or just a value of 1 is good is judged based upon the data mean. Hence, a term called scatter index (SI) is defined to judge whether RMSE is good or not. SI is RMSE normalised to the measured data mean or SI=RMSE/measured data mean. If SI is less than one, your estimations are acceptable.
Hi MM Ali,
I searched for scatter index everywhere else in the internet but i did not get anything.
Can you send some reference where I can study more about it
Also do you know if there is a python library that helps me calculate this value?
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.724.9537&rep=rep1&type=pdf
Hi Karen,
Thanks for all the great posts from you & the Analysis Factor Team!
Could you clarify a position on RMSE vs. RSE? When I first learned of them, they seemed to be used interchangeably on various stats sites. Took me awhile of web-digging to parse out the difference. They share the same formula, but RMSE divides by n and RSE divides by n-2. From what I read, that makes the RSE unbiased, with the more conservative sample estimation and RMSE leaning biased with the lower estimate value. If this true, why might many websites mention RMSE and not the RSE, and moreover, why might some sites use them interchangeably if there is a difference? How would you contrast the RSE to your post above on the RMSE?
Thanks!
Hi, I am currently doing research on African countries and their sovereign credit ratings (it is my independent variable). I need to do a panel regression on my data. Some of the countries have the same SCR throughout the period of review – I have decided to leave them out as they are not helpful in the regression. Is there some sort of literature that confirms this? that you leave out independent variables that have no change during the regression timeline? Thanks
Hi Karen,
The following are the values for my dataset. Can you please tell if this is a good fit or not?
Thanks
RMSE
[1] 0.9495382
> sd(y)
[1] 0.6271138
Hi Nishant,
Yes, It seems good. But again it depends on your Business domain. And Data Set. 1.2 something RMSE AND MSE score is also good but again as i said “it depends on your Data set”- I hope it clears your doubt.
Hi Karen,
Can I use this article as a reference and if I have to use it, would you mind to provide a publication year and maybe some reference sources such as books and other scientific articles.
Thanks
Hi Hashim,
You’re welcome to use it as a reference. I am pretty sure for web pages the appropriate year is not publication year but when you downloaded it, since they can be changed at any point.
Hi Karen,
Thanks for this useful explanation.
I have one question regarding how to evaluate an RMSE in predictive regression.
What criteria are used? For example if you find a RMSE which is about the same as the standard deviation of the dependent variable, is that then good? How can you evaluate whether the RMSE/prediction error is small enough or not?
Dina, the RMSE is essentially the standard deviation of what the model doesn’t explain. So if it’s close to the std deviation of Y, then the model isn’t explaining very much.
Hi, how do I calculate the error range for the RMSE value from the curve fittin toolbox. I have 17 coefficients and i want an error range fir each of the 17 values.
After conducting a a linear analysis. RMSE obtained is 1.8 with R-square can i use the model with this value of RMSE. can any 1 tell me the acceptance range of RMSE.
Hi Karen,
Really nice explanation! Clear and solid!
I would like to cite your work in my assignment, though it follows APA style when referencing. So do you mind to provide me with the initial of your first name and the year you performed the analysis (I’m assuming it was 2013, judging from the oldest comment)?
Thank you!
Hi am doing some modelling project and after calculating my parameter estimates, I end up with RMSE value of 87.4984.Does this indicate a good fit?
Thanks
That value of RMSE is large not to explain a good fit,, rather a lower value of RMSE a good fit,,atleast 0.10 to 0.15
Hi,
I applied Neural Network analysis. Could you please quide me about that If the value of RMSE is 0.065? Is it good fit or not. Or under fit.
Kindly email Your answer.
Dear Karen
What if the model is found not fit, what can we do to enable us to do the analysis?
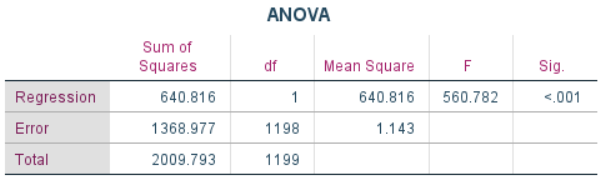
I have two regressor and one dependent variable. when I run multiple regression then ANOVA table show F value is 2.179, this mean research will fail to reject the null hypothesis. what should I do now, please give me some suggestions
can we use MSE or RMSE instead of standard deviation in sharpe ratio
Your first sentence is “A well-fitting regression model results in predicted values close to the observed data values.” If this is the purpose of the model, then there are other criteria that are better and they apply regardless of the method for fitting an equation. These include mean absolute error, mean absolute percent error and other functions of the difference between the actual and the predicted.
Thus, before you even consider how to compare or evaluate models you must a) first determine the purpose of the model and then b) determine how you measure that purpose. For (b), you should also consider how much of an error is acceptable for the purpose of the model and how often you want to be within that acceptable error.
Just using statistics because they exist or are common is not good practice.
Hi Karen,
I think you made a good summary of how to check if a regression model is good. Those three ways are used the most often in Statistics classes. For the R square and Adjust R square, I think Adjust R square is better because as long as you add variables to the model, no matter this variable is significant or not, the R square will become larger any way. So you cannot justify if the model becomes better just by R square, right?
Ruoqi, Yes, exactly. Adj R square is better for checking improved fit as you add predictors
Is it possible to get my dependent variable by summing up all the sets of independent variables? Please your help is highly needed as a kind of emergency. Thank you and God Bless.
Hi Bn Adam,
No, it’s not.
Hi! am using OLS model to determine quantity supply to the market, unfortunately my r squared becomes 0.48. what can i do to increase the r squared, can i say it good??
hi,
how method to calculat the RMSE, RMB
betweene 2 data Hp(10) et Hr(10)
thank you
Suppose I have the following data:
3 5 7 8 4 10 11 13 12
And I need to calculate corresponding “predicted values” for every data.
How do I do so? I need to calculate RMSE from above observed data and predicted value.
I have read your page on RMSE (https://www.theanalysisfactor.com/assessing-the-fit-of-regression-models/) with interest. However there is another term that people associate with closeness of fit and that is the Relative average root mean square i.e. % RMS which = (RMS (=RMSE) /Mean of X values) x 100
However I am strugging to get my head around what this actually means . For example a set of regression data might give a RMS of +/- 0.52 units and a % RMS of 17.25%. I understand how to apply the RMS to a sample measurement, but what does %RMS relate to in real terms.?
Hi Roman,
I’ve never heard of that measure, but based on the equation, it seems very similar to the concept of coefficient of variation.
In this context, it’s telling you how much residual variation there is, in reference to the mean value. It’s trying to contextualize the residual variance. So a residual variance of .1 would seem much bigger if the means average to .005 than if they average to 1000. Just one way to get rid of the scaling, it seems.
Hi Karen
I am not sure if I understood your explanation.
In view of this I always feel that an example goes a long way to describing a particular situation. In the example below, the column Xa consists if actual data values for different concentrations of a compound dissolved in water and the column Yo is the instrument response. The aim is to construct a regression curve that will predict the concentration of a compound in an unknown solution (for e.g. salt in water) Below is an example of a regression table consisting of actual data values, Xa and their response Yo. The column Xc is derived from the best fit line equation y=0.6142x-7.8042
As far as I understand the RMS value of 15.98 is the error from the regression (best filt line) for a measurement i.e. if the concentation of the compound in an unknown solution is measured against the best fit line, the value will equal Z +/- 15.98 (?). If this is correct, I am a little unsure what the %RMS actually measures. The % RMS = (RMS/ Mean of Xa)x100?
Any further guidance would be appreciated.
from
trendline
Actual Response equation
Xa Yo Xc, Calc Xc-Xa (Yo-Xa)2
1460 885.4 1454.3 -5.7 33.0
855.3 498.5 824.3 -31.0 962.3
60.1 36.0 71.3 11.2 125.3
298 175.5 298.4 0.4 0.1
53.4 22.4 49.2 -4.2 17.6
279 164.7 280.8 1.8 3.4
2780 1706.2 2790.6 10.6 112.5
233.2 145.7 249.9 16.7 278.0
Xm = 752.375 454.3 752.3 sum = 1532.2
SD.S = RMS=√(sum x residuals squared)/(N-2)= ±15.98
%rel RMS = (RMS/Xm)*100= ± 2.12
slope =0.6142
Y – intercept=-7.8042
I think what she tried to explain is the following:
You have a RMS value of, say, 2 ppm.
If the concentration levels of the solution typically lie in 2000 ppm, an RMS value of 2 may seem small. So, in short, it’s just a relative measure of the RMS dependant on the specific situation.
An alternative to this is the normalized RMS, which would compare the 2 ppm to the variation of the measurement data. So, even with a mean value of 2000 ppm, if the concentration varies around this level with +/- 10 ppm, a fit with an RMS of 2 ppm explains most of the variation.
I know i’m answering old questions here, but what the heck.. 🙂
Hi Roman,
You raised a very good point. Suppose you are estimating the minimum temperature of a place where its variation is 0-5 C. Then if your RMSE is around 1, your estimations are good. But if you are estimating the mean sea level pressure of the same region expecting to get the RMSE of 1 is something like a kid asking for the moon. In this case, an RMSE of a few hundred is good enough. Now, to judge whether your SMSE of a few hundred is good or just a vaue of 1 is good is judged based upon the data mean. Hence, a term called scatter index (SI) is defined to judge whether RMSE is good or not. SI is RMSE normalised to the data mean or SI=RMSE/measured data mean. If SI is less than one, your estimations are acceptable.
Hi,
I wanna report the stats of my fit. if i fited 3 parameters, i shoud report them as: (FittedVarable1 +- sse), or (FittedVarable1, sse)
thanks
Hi Karen,
Yet another great explanation.
Regarding the very last sentence – do you mean that easy-to-understand statistics such as RMSE are not acceptable or are incorrect in relation to e.g., Generalized Linear Models? Or just that most software prefer to present likelihood estimations when dealing with such models, but that realistically RMSE is still a valid option for these models too?
Thanks!!!
Hi Grateful,
Hmm, that’s a great question. My initial response was it’s just not available–mean square error just isn’t calculated. But I’m not sure it can’t be. The residuals do still have a variance and there’s no reason to not take a square root. And AMOS definitely gives you RMSEA (root mean square error of approximation). Perhaps that’s the difference–it’s approximate. I will have to look that up tomorrow when I’m back in the office with my books. 🙂
Thanks, Karen. Looking forward to your insightful response.
There is lots of literature on pseudo R-square options, but it is hard to find something credible on RMSE in this regard, so very curious to see what your books say. 🙂
Thanks again.