Imagine this scenario:
This year’s flu strain is very vigorous. The number of people checking in at hospitals is rapidly increasing. Hospitals are desperate to know if they have enough beds to handle those who need their help.
You have been asked to analyze a previous year’s hospitalization length of stay by people with the flu who had been admitted to the hospital. The predictors in your data set are age group, gender and race of those admitted. You also have an indicator that signifies whether the hospital was privately or publicly run.
(more…)
Many who work with statistics are already functionally familiar with the normal distribution, and maybe even the binomial distribution.
These common distributions are helpful in many applications, but what happens when they just don’t work?
This webinar will cover a number of statistical distributions, including the:
- Poisson and negative binomial distributions (especially useful for count data)
- Multinomial distribution (for responses with more than two categories)
- Beta distribution (for continuous percentages)
- Gamma distribution (for right-skewed continuous data)
- Bernoulli and binomial distributions (for probabilities and proportions)
- And more!
We’ll also explore the relationships among statistical distributions, including those you may already use, like the normal, t, chi-squared, and F distributions.
Note: This training is an exclusive benefit to members of the Statistically Speaking Membership Program and part of the Stat’s Amore Trainings Series. Each Stat’s Amore Training is approximately 90 minutes long.
(more…)
Pretty much all of the common statistical models we use, with the exception of OLS Linear Models, use Maximum Likelihood estimation.
This includes favorites like:
That’s a lot of models.
If you’ve ever learned any of these, you’ve heard that some of the statistics that compare model fit in competing models require (more…)
It’s that time of year: flu season.
Let’s imagine you have been asked to determine the factors that will help a hospital determine the length of stay in the intensive care unit (ICU) once a patient is admitted.
The hospital tells you that once the patient is admitted to the ICU, he or she has a day count of one. As soon as they spend 24 hours plus 1 minute, they have stayed an additional day.
Clearly this is count data. There are no fractions, only whole numbers.
To help us explore this analysis, let’s look at real data from the State of Illinois. We know the patients’ ages, gender, race and type of hospital (state vs. private).
A partial frequency distribution looks like this: (more…)
In a previous article, we discussed how incidence rate ratios calculated in a Poisson regression can be determined from a two-way table of categorical variables.
Statistical software can also calculate the expected (aka predicted) count for each group. Below is the actual and expected count of the number of boys and girls participating and not participating in organized sports.
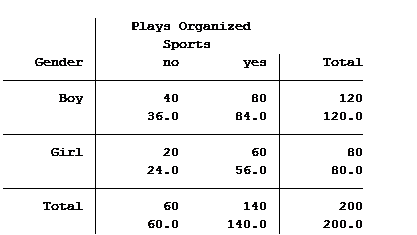
The value in the top of each cell is the actual count (40 boys do not play organized sports) and the bottom value is the expected/predicted count (36 boys are predicted to not play organized sports).
The Poisson model that we ran in the previous article generated the following table: (more…)
The coefficients of count model regression tables are shown in either logged form or as incidence rate ratios. Trying to explain the coefficients in logged form can be a difficult process.
Incidence rate ratios are much easier to explain. You probably didn’t realize you’ve seen incidence rate ratios before, expressed differently.
Let’s look at an example.
A school district was interested in how many children in their sixth grade classes played on organized sports teams. So they did a count and also noted the gender of the child. The results were put into a table: (more…)